L'obiettivo di questa pagina è duplice:
- da un lato vogliamo fornire i concetti base di calcolo delle probabilità indispensabili per la comprensione del gioco della roulette;
- dall'altro è altresì importante applicare le leggi della probabilità alla roulette, con esempi concreti e tabelle autoesplicative.
Questa guida vuole quindi essere una sorta di "corso accelerato di calcolo delle probabilità applicato al gioco della roulette". Non abbiate paura, è gratuito!
Esposizione dei concetti fondamentali di calcolo delle probabilità
Concetti di probabilità applicata alla roulette
La teoria della probabilità nel gioco reale della roulette: teoria, pratica e falsi miti
Tipologie e categorie, significati
Applicazioni alla roulette
Significato, esempi
Concetti base di calcolo della probabilità
CLICCA QUI per saltare la parte teorica di probabilità e passare direttamente alla parte pratica.
In questa parte presentiamo le basi essenziali di calcolo della probabilità, nozioni che torneranno utili per capire alcuni concetti che sono il fondamento delle probabilità applicate alla roulette (come ad esempio la diatriba sul fatto che la roulette non abbia memoria e che le estrazioni siano davvero indipendenti le une dalle altre).
Preambolo sugli eventi
Gli eventi sono accadimenti per i quali ci si può chiedere se sono FALSI o VERI:
- E1 = alla roulette è uscito un numero pari
- E2 = alla roulette è uscito il numero pieno 15
Quando si parla di eventi e di probabilità, un concetto logico molto importante è quello dell'implicazione:
Un evento E1 implica un evento E2 se dalla verità di E1 discende la verità di E2.
Detta in altre parole, E1 implica E2 se al verificarsi dell'evento E1 consegue obbligatoriamente il verificarsi dell'evento E2.
Per fare un esempio concreto:
- E1 = alla roulette è uscito il numero 4
- E2 = alla roulette è uscito un numero nero
E1 -> E2 (si legge E1 implica E2)
Per dirla in parole: l'evento "alla roulette è uscito il 4" implica che alla roulette è uscito un numero nero, dato che sappiamo per certo che il numero quattro è infatti di colore nero.
Quando si analizzano gli eventi e le probabilità che ne conseguono, è altresì di fondamentale importanza capire i concetti di UNIONE e di INTERSEZIONE di eventi:
- intersezione di eventi: evento che è vero se entrambi gli eventi sono veri ed è falso se se almeno uno di essi è falso
- è uscita la prima dozzina
- è uscita la prima colonna
- unione di eventi: evento che è vero se almeno uno di essi è vero ed è falso se entrambi sono falsi
- è uscita la prima dozzina
- è uscita una certa colonna
A volte ci viene anche molto utile ragionare con la negazione di un evento.
La negazione di un evento è un nuovo evento che:
- è vero se l'evento di cui è negazione è falso
- è falso se l'evento di cui è negazione è vero
Ad esempio se un evento è "è uscito il 6", la sua negazione è "è uscito un qualsiasi altro numero".
Per capire anche tutta una vasta serie di casistiche è necessario comprendere il concetto di compatibilità e incompatibilità di eventi.
Due eventi sono incompatibili se il verificarsi dell'uno esclude l'altro.
Ne consegue che l'intersezione di due eventi incompatibili è nulla.
Dobbiamo anche definire eventi impossibili ed eventi aleatori:
- evento impossibile: evento che non può verificarsi
- evento aleatorio: evento per il quale non si può dire se è vero o falso
Un esempio di evento impossibile è "uscirà il 4 rosso" (non è possibile perché il 4 è per definizione nero).
Un esempio di evento aleatorio: "lanciando la pallina uscirà il 7".
La probabilità
Siamo ora pronti per una prima definizione di Probabilità di un evento.
La Probabilità indica la facilità con cui si verifica un evento aleatorio.
In matematica la probabilità P di un evento aleatorio E si indica con P(E) (la 'P' è maiuscola).
Nel caso di roulette non truccata in cui tutti gli eventi sono ugualmente possibili, la Probabilità si calcola come il rapporto di casi favorevoli rispetto a tutti i casi possibili.
La Probabilità è un numero compreso tra 0 e 1. Siamo infatti soliti ad esprimerla in percentuale.
Ad esempio studiamo il seguente evento E = "uscirà il numero 14".
Casi favorevoli: 1
Casi possibili: 37
Abbiamo quindi che la probabilità che esca il numero 14 è di 0.027 (ovvero del 2.7%).
Un'importante proprietà della probabilità è che la somma delle probabilità di tutti gli eventi disgiunti è 1.
Ad esempio, parlando sempre dei numeri pieni, si ha che ci sono 37 eventi equiprobabili: la probabilità che esca il numero 0 è uguale alla probabilità che esca il numero 1 che è uguale alla probabilità che esca un qualunque numero pieno.
La probabilità di ogni singolo evento è, come visto sopra, di 0.027, la somma di tutte queste 37 probabilità è esattamente 1.
La probabilità della negazione di un evento (o anche la probabilità dell''evento contrario) è invece data da 1-P(E).
Se quindi la probabilità che esca il numero 28 è di 0.027 la probabilità che esca un qualunque altro numero è di 1-0.027 = 0.973
Vediamo ora altre nozioni fondamentali di probabilità in base al tipo di evento, nozioni davvero utili nel gioco della roulette.
Probabilità dell'unione di eventi (Probabilità totale)
- Probabilità di eventi incompatibili:
Un esempio di probabilità totale su eventi incompatibili è dato da "Probabilità che esca la terzina 1-2-3 oppure il numero 14". Sono eventi incompatibili perchè non si possono verificare contemporaneamente.
P(A) = probabilità che esca la terzina 1-2-3 = 3/37
P(B) = probabilità che esca il numero 14 = 1/37
- Probabilità di eventi compatibili:
Un esempio di probabilità su eventi compatibili è ad esempio la "Probabilità che esca la terzia 1-2-3 o una colonna". Gli eventi sono compatibili perchè possono verificarsi contemporaneamente.
P(A) = probabilità che esca la terzina 1-2-3 = 3/37
P(B) = probabilità che esca una colonna = 12/37
P(intersezione) = 1/37
Probabilità dell'intersezione di eventi
In questo caso è necessario distinguere se gli eventi sono dipendenti o indipendenti tra di loro.
- Probabilità di eventi indipendenti:
Ad esempio la probabilità che esca prima il numero 8 e poi il numero 36 è 1/37 * 1/37 = 0.07%
- Probabilità di eventi dipendenti:
Viene anche utile la definizione di variabile casuale.
Si dice variabile casuale X una variabile che può assumere i valori x1, x2 , ..., xn
al verificarsi di eventi casuali, incompatibili e complementari E1, E2, ..., En
le cui probabilità sono uguali a p1, p2 , ..., pn
L'insieme dei valori p1, p2 , ..., pn costituisce la distribuzione di probabilità.
La distribuzione di probabilità dei numeri che escono alla roulette è uniforme.
Strettamente correlata è la definizione di valor medio.
Il valor medio E di una variabile casuale è uguale alla somma dei prodotti dei valori che assume la variabile casuale per le rispettive probabilità
Riguardo alle variabili aleatorie, definiamo il concetto di indipendenza di variabili aleatorie.
2 variabili aleatorie X e Y sono indipendenti se se per tutte le coppie di valori xi , yi corrispondenti a due determinati eventi la probabilità che si verifichino entrambi risulta:
pij = pi * pj
Detto in altre parole conoscere qualcosa riguardo al valore di una di esse non apporta alcuna informazione circa la conoscenza del valore dell'altra.
Il concetto di frequenza
Possiamo introdurre il concetto di frequenza come rapporto tra numero di successi e numero di prove eseguite.
Analogamente alla probabilità, la frequenza ha un valore compreso tra 0 e 1 (o come più comunemente siamo soliti a ragionare, tra lo 0% e il 100%).
La differenza sostanziale è che la probabilità si calcola a priori, mentre la frequenza a posteriori.
Essendo molto poco formali e poco precisi possiamo dire che la probabilità è un dato teorico, la frequenza un dato pratico.
All'aumentare del numero di prove ci si può ragionevolmente aspettare che la frequenza con cui si manifesta effettivamente un evento tenda alla probabilità teorica calcolata a priori associata alla realizzazione di quell'evento. Per un numero successivamente grande di prove la frequenza tende ad assumere il valore della probabilità.
Ad esempio se consideriamo il lancio della pallina sulla roulette e l'evento della vittoria associato all'uscita di un numero ad esempio il 13, quanto detto prima può essere così contestualizzato: la probabilità teorica che esca un certo numero ad esempio il 13 è 1/37 = 2.7%; se eseguiamo il lancio un numero sufficientemente grande di volte, supponiamo milioni di volte, tendenzialmente la frequenza di uscita del 13 al di la delle oscillazioni sarà 1/37 = 2.7%.
Nulla vieta naturalmente che il 37 non esca mai anche per migliaia di volte, anche se altamente improbabile.
Per trovare una correlazione connessione tra frequenza e probabilità viene in nostro aiuto la legge dei grandi numeri.
La legge dei grandi numeri
La legge dei grandi numeri, semplificata all'osso (e speriamo che Bernoulli non se la prenda), sostiene che al tendere all'infinito del numero di una sequenza di prove indipendenti ed equiprobabili di una variabile casuale, la media calcolata della sequenza converge alla media teorica.
Legge forte dei grandi numeri
Data una successione di variabili aleatorie X1, X2, ..., Xn indipendenti ed ugualmente distribuite con media μ, definita la media calcolata come
allora la media calcolata (media campionaria) converge quasi certamente alla media comune.
Approfondimenti sulla legge dei grandi numeri su Wikipedia.
Detto in maniera poco rigorosa ma molto esplicativa per il lettore che ha meno confidenza con il formalismo matematico, si ha che su un grande numero di esperimenti (lanci), il valor medio tenderà al valor medio teorico.
Se si preferisce (come già detto nel paragrafo precedente) si può dire che la frequenza di realizzazione di un evento tende alla probabilità teorica che quell'evento si manifesti.
Quest'ultima affermazione discende direttamente dalla legge dei grandi numeri, di seguito un ragionamento che permette di asserire questo.
In un gioco qualunque come ad esempio la roulette, costruiamo la seguente variabile aleatoria X che assume 2 valori possibili:
dove p rappresenta dunque la frequenza teorica con cui si realizza la vittoria
In base alla definizione di valor medio possiamo calcolare che
quindi il μ presente nell'enunciato del teorema è pari a p.
Supponiamo di giocare n volte allo stesso modo. A ogni lancio le variabili aleatorie che descrivono la situazione sono tra loro identiche, sono costruite nello stesso modo, lo spazio degli eventi è lo stesso, analogamente le distribuzioni di probabilità.
Allora potendo applicare la legge dei grandi numeri abbiamo che tende alla probabilità p.
Ma se X=1 in caso di vittoria e X=0 in caso di sconfitta, allora è per definizione è proprio la frequenza con cui si è manifestata la vittoria.
Forti di quanto detto si può capire perché esista anche una definizione frequentistica del concetto di probabilità secondo cui la probabilità di un evento sarebbe la frequenza calcolata su un numero sufficientemente alto di prove.
Le probabilità nella roulette: teoria, pratica e falsi miti
Abbiamo visto finora molti concetti teorici e pochi esempi. Nel prossimo paragrafo parleremo per esempi concreti, ora però ci preme spiegare a parole alcuni concetti di fondamentale importanza nella decisione se giocare alla roulette o no.
Le estrazioni indipendenti - La roulette non ha memoria
Si tenga presente che la roulette è un gioco senza memoria: a ogni giro quello che succede è indipendente da eventi passati.
Supponiamo che siano usciti n rossi consecutivi; al lancio n+1 la probabilità che esca ancora un rosso è sempre la stessa: P("esce rosso") = 18/37.
Ogni evento è quindi indipendente da quello passato.
Abbiamo in precedenza già esposto la legge dei grandi numeri, per quello che interessa a noi nel gioco della roulette: all'aumentare delle estrazioni, la frequenza media prevista nel verificarsi di un evento tende a coincidere con il valore teorico di probabilità.
Questo teorema da un lato dà forza a tutta la teoria della probabilità applicata alla roulette, ma dall'altro apre le porte a cattive interpretazioni e a luoghi comuni.
Se è uscito rosso 10 volte di fila, è improbabile che esca rosso ancora una volta! => FALSO MITO
Visto che con l'aumentare del numero di estrazioni ci si aspetta che la frequenza media tenda a coincidere con la probabilità, ci aspetteremmo un certo equilibrio degli eventi.
Il giocatore poco matematico infatti è portato a credere che a causa della legge dei grandi numeri il sistema tenda all'equilibrio: se è uscito nero 20 volte di fila, è quasi impossibile che esca ancora nero dato che la probabilità che esca un colore è quasi del 50%!
Questo è un madornale errore di interpretazione, dato che la roulette non ha memoria di quanto è successo nelle 20 estrazioni precedenti: dopo 20 neri le probabilità sono sempre le stesse:
- P("esce nero") = 18/37
- P("esce rosso") = 18/37
- P("esce lo zero") = 1/37
I numeri ritardatari nella roulette
Analogo discorso può essere fatto per i cosiddetti "numeri ritardatari": se un numero non è uscito per 100 volte, si potrebbe essere portati a pensare: il ritardatario uscirà a breve? In realtà la probabilità di estrazione del pieno è sempre 1/37, indipendentemente da quanto ritardo abbia accumulato.
Si può invece ragionevolmente dire che su un numero sufficientemente grande di estrazioni le frequenze relative ai vari numeri tendono a livellarsi su una stessa percentuale: dopo 1000000000 lanci, è verosimile che le frequenze relative allo 0, all' 1, al 2, al 3, al 36 si attestino tutte attorno a 2,7% ovvero a 1/37.
La roulette francese non è un gioco equo
Un'ultima trattazione prima di passare agli esempi di probabilità con tabelle: cerchiamo di capire se a livello matematico la roulette sia un gioco equo oppure no.
Innanzitutto diamo la definizione di gioco equo:
un gioco è equo quando il valor medio E(X) delle sue vittorie e sconfitte, in generale dei suoi risultati è 0.
Dunque, un gioco X è:
- equo se E(X)=0
- vantaggioso se E(X)>0
- in perdita se E(X)<0
Dato l'insieme dei possibili risultati con associate le probabilità di realizzazione
Ora il punto è che per la legge dei grandi numeri giocando infinite volte a un medesimo gioco il valor medio tende al valor medio teorico.
Quindi:
- giocando infinite volte a un gioco equo si va incontro a vittoria nulla;
- giocando infinite volte a un gioco vantaggioso si va incontro a sicura vincita;
- giocando infinite volte a un gioco in perdita si va incontro a sicura perdita.
Riesaminiamo come è fatta la roulette francese, o meglio consideriamo sopratutto quali sono le vincite associate agli eventi.
Supponiamo di aver puntato un gettone sull'uscita di un numero che esce con probabilità p1 = 1/37 , in caso di vincita si ottiene una vincita effettiva x1 = 35 ; in caso di perdita il giocatore perde il singolo gettone x2 = -1 cosa che avviene con probabilità p2 = 36/37 .
E(X) = p1x1 + p2x2
ovvero
La roulette francese non è un gioco equo.
Come cambierebbero le cose se non ci fosse lo zero?
La roulette senza zero è un gioco equo.
E cosa accadrebbe se la vincita fosse 36 pezzi anzichè 35?
La roulette con 36 pezzi di vincita sul pieno è un gioco equo.
Dunque la struttura del tavolo congiuntamente all'entità delle vittorie e delle sconfitte date per definizione, facenti parte delle regole del gioco, determinano che la roulette non sia un gioco equo bensì un gioco in perdita.
Dalla parte del banco chiaramente il gioco è vantaggioso, nelle medesime condizioni i flussi di cassa per il banco cambiano segno e risulterebbe
Quanto esposto per una giocata di un gettone su singolo numero in verità vale sempre, per il tipo di giocate esposte in questo sito: cavalli, terzine, sestine, dozzine ecc e anche aumentando la posta in gioco, sono sempre dei giochi vantaggiosi a favore del banco.
Se io giocatore gioco n volte, anche in modo diverso di volta in volta puntando su terzine ,dozzine, combinate ecc, queste giocate sono tra loro indipendenti e il valor medio di n variabili aleatorie indipendenti tra loro, aventi ognuna media negativa differente, tenderà nuovamente a un valore negativo.
E allora perchè giochi alla roulette?
Gioco alla roulette perchè, pur consapevole che non sia un gioco equo, mi diverto a giocarci cercando il sistema migliore per limitare le perdite e, con l'aiuto della fortuna, per qualche piccola vincita che mi permetta di giocare gratuitamente la volta successiva o uscire a cena con la moglie/fidanzata.
Le tabelle delle probabilità
Abbiamo fatto una trattazione inizialmente teorica, quindi un po' più esplicativa. Andiamo ora a fare un po' di esempi, sintetizzandoli in delle tabelle molto chiare.
Si noti che, essendo le tabelle molto larghe, se visualizzate il sito da un dispositivo mobile queste saranno ridotte ai minimi termini. Si consiglia quindi la visione da un pc Desktop per avere una visione completa del calcolo delle probabilità di queste tabelle sulle giocate della roulette.
Iniziamo a vedere la tabella delle probabilità di una singola giocata.
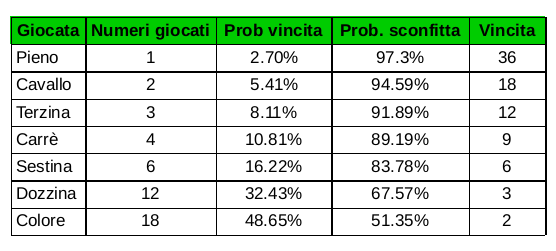
ATTENZIONE: sezione in aggiornamento
E' semplicissima chiunque potrebbe farla, ve la mostriamo cosìcchè possiate analizzarla e vederla:
| Giocata | Numeri giocatinum gioc | Numeri roulettenum roul | % vincita | Pagata |
|---|---|---|---|---|
| Pieno | 1 | 37 | 2,70% | 1 to 36 |
| Cavallo | 2 | 37 | 5,41% | 1 to 18 |
| Terzina | 3 | 37 | 8,11% | 1 to 12 |
| Carrè | 4 | 37 | 10,81% | 1 to 9 |
| Sestina | 6 | 37 | 16,22% | 1 to 6 |
| Dozzina | 12 | 37 | 32,43% | 1 to 36 |
| Chance semplice | 18 | 37 | 48,65% | 1 to 2 |
La sua lettura è facile, ad ogni tipo di giocata è associato un numero che non è il numero sul tavolo ma il totale dei numeri che si giocano. Quindi una sestina gioca 6 numeri diversi tra loro e non il numero 6. Continuando a leggere la riga ad ogni giocata corrisponde una percentuale calcolata semplicemente dividendo il numero dei numeri giocati (scusate il gioco di parole forzato) con 37 che sono i numeri totali della roulette francese (ovviamente in quella americana le percentuali cambiano perchè sono su 38 numeri invece che 37). La colonna "pagata" indica il numero di fiches che si vincono scommettendone una su quella giocata.
Ed ecco che il gioco è fatto, da qui in poi si possono fare mille ragionamenti su come giocare. Noi ve ne proporremo qualcuno ma il consiglio è di usare questa tabella anche quando vi informate sulle strategie che abbiamo scritto.
Qui di seguoto trovate una tabella simile alla predente e uguale alla tabella della pagina delle regole della roulette, che per alcuni può essere più esaustiva:
| Nome puntata | Numeri coperti (n)num gioc | Vincita (36/n-1)net win | Pagamento (inclusa la posta)tot win | Prob (n/37) |
|---|---|---|---|---|
| Pieno | 1 | 35 | 36 | 2,70% |
| Cavallo | 2 | 17 | 18 | 5,41% |
| Terzina | 3 | 11 | 12 | 8,11% |
| Carrè | 4 | 8 | 9 | 10,81% |
| Quattro Primi | 4 | 8 | 9 | 10,81% |
| Sestina | 6 | 5 | 6 | 16,22% |
| Colonna | 12 | 2 | 3 | 32,43% |
| Dozzina | 12 | 2 | 3 | 32,43% |
| Rosso/Nero | 18 | 1 | 2 | 48,65% |
| Pari/Dispari | 18 | 1 | 2 | 48,65% |
| Passe/Manque | 18 | 1 | 2 | 48,65% |
Trend e probabilità
Tornando al discorso di prima, queste percentuali potrebbero subire delle variazioni in positivo o negativo se si associano ai trend delle chance semplici. Non stiamo a dilungarci su calcoli difficili e per ai più incomprensibili, ma facciamo un semplice esempio.
Immaginiamo di aver guardato molte estrazioni e aver indivduato un pattern (modello) sulle uscite dei rossi e dei neri e quindi riuscite a sapere quasi con certezza che la prossima estrazione sarà un numero rosso. A questo punto la tabella delle probabilità cambia, perchè i numeri in gioco non sarebbero più 37 ma solo 19 (abbiamo tolto i 18 nnumeri neri), ecco come la tabella viene fuori.
| Giocata | Numeri giocatinum gioc | Numeri roulettenum roul | % vincita | Pagata |
|---|---|---|---|---|
| Pieno | 1 | 19 | 5,26% | 1 to 36 |
| Cavallo | 2 | 19 | 10,53% | 1 to 18 |
| 1 to 12 | ||||
| 1 to 9 | ||||
| 1 to 6 | ||||
| 1 to 36 | ||||
| Chance semplice | 18 | 19 | 94,74% | 1 to 2 |
C'è da notare però che molte puntate non possono essere effettuate in questo caso perchè, come vedete dalla tabella, non esistono terzine, carrè, sestine e dozzine con solo numeri rossi, ma al loro interno avranno numeri neri e quindi dovremmo analizzarle ognuna in modo da trovare i colori giusti e quindi cambiare le probabilità, insomma avete capito che non ne usciamo più vivi.
Ma in questo caso giocare il numero pieno si passa dal 2,7% al 5,3% di probabilità di vincere, o giocare il cavallo (ma solo 9-12, 16-19, 18-21 e 27-30) si passa da circa il 5% al 10% mentre ovviamente la chance semplice (in questo caso giocare il rosso) avrà una probabilità di vincita vicino al 100% (ovviamente non è 100 perchè c'è lo zero).
Lo stesso tipo di ragionamento possiamo farlo se abbiamo la certezza che esca un numero pari o dispari oppure una dozzina o un numero compreso tra 1-18 o 19-36.
Le giocate combinate
Le giocate combinate che intendiamo in questo paragrafo si riferiscono a casi in cui si può vincere tanto, rischiando qualcosa di più ma non mutando sostanzialmente le probabilità di vincere.
Le tabelle che avete visto fino ad ora prendevano come esempio tutti i tipi di giocata, ma presi singolarmente. E se invece iniziassimo a prevedere delle giocate combinate, cioè uniamo i vari tipi di giocata? Le cose cambiano e di molto, come potete vedere nella seguente tabella:
| Giocata 1g1 | Giocata 2g2 | Pezzi giocatipz | Vince 1v1 | Vince 2v2 | Vin totvtot | % vincita %v |
|---|---|---|---|---|---|---|
| Pieno | Terzina | 2 | 36 | 12 | 54 - 2 | 2,7% |
| Cavallo | Terzina | 2 | 18 | 12 | 30 - 2 | 5,4% |
| Terzina | Sestina | 2 | 9 | 12 | 21 - 2 | 10,8% |
| Ses | Sestina | 2 | 12 | 6 | 18 - 2 | 16,2% |
La tabella si legge così: giocata 1, 2 (g1, g2) sono le singole giocate che combiniamo sulla stessa linea (pieno e cavallo si gioca un pezzo sul cavallo e un pezzo su uno dei due pieni sul cavallo); pezzi giocati (pz) sono il numero di fiches totali giocate supponendo che a ogni giocata si punta un pezzo; vince 1, 2 (v1, v2) sono le vincite della singola giocata; Vin tot è la somma delle due vincite nel caso quindi combinato;
cav = cavallo; ter = terzina; ses = sestina
Come potete vedere dalla tabella le percentuali di viinctia di queste combinazioni coincidono con le percentuali di vincita delle singole giocate (prima giocata). Qui si punta però una fiches in più e alla stessa probabilità si vincono più fiches. Ovviamente la probabilità diminuisce all'aumentare del numero di fiches che si vincono. Poniamo ad esempio la prima giocata combinata (pieno e cavallo), per vincere 54 - 2 pezzi netti cioè 52 pezzi giocandone due, si ha il 2,7% di possibilità. Per cui portei essere disposto a giocare questa combinata 27 volte per prendere 1 numero su 37. Ovviamente giocando 1 solo pezzo potrei giocare 37 volte per almeno pareggiare, ma se vinco ottengo meno fiches.
Leggendo la tabella in €, ponendo che 1 pezzo sia uguale a 5€, puntando 10€ ho il 16,2% di probabilità di vincere 80€ netti e il 2,7% di vincere 260€ netti, non male!
Se si volesse calcolare la probabilità di vincita di almeno una delle due giocate, le probabilità cambierebbero, aumenterebbero sensibilmente, ma le fiches che si vincono sarebbero meno.
Di esempi come questi se ne potrebbero fare a centinaia ed è uno dei motivi che rende la roulette così affascinante, l'ideale sarebbe quello di trovare un equilibrio tra giocate e relativi payout, ma poi si sa, ognuno gioca a suo modo e alla fine la fortuna ci vuole sempre.
Le probabilità di ripetizione di un numero
Ci sono alcuni che credono che esistano delle probabilità che un numero esca due volte di fila a seconda del verificarsi di determinati requisiti. Entriamo in un campo complicatissimo e a cui noi crediamo poco anche perchè, per come siamo abituati a giocare, tutte o una parte delle fiches vincenti la lasciamo sul tavolo, per cui se esce di nuovo lo stesso numero siamo lo stesso vincenti.







